6th dimensional array algorithm
Back in 1977 real computers still digested punch cards and spit out answers on continuous reams of paper. That was also a year in which numerous small personal computers entered the market. I was to purchase an Apple II in 1978 and when not at work offshore in the Gulf of Mexico, spent my time learning to program the thing. There was little alternative to programming in those days as software for Apples and Z-80 based counterparts was very sparse and came only on cassette tapes. Phone modems, the Internet, hard disk and even floppy disk drives for these new PCs did not exist yet.
From a page published in “Best of Creative Computing” (Vol 1, 1976, p.185) I was to encounter a complicated and intriguing logic puzzle that was to strain my thinking capacity in the years to come. Solving the puzzle is a small challenge in itself but I became obsessed with programming an algorithm that could solve the puzzle. It was a struggle but my auto-didactic approach in making the PC solve the puzzle, eventually worked. Declarative programming styles like constraint satisfaction programming might have been better applied to such a puzzle, had they existed at the time.
Fast forwarding to the present, a multitude of Web pages and blogs address this puzzle, in one or another of its various forms. Even Wikipedia, after these many years, now has a page for the puzzle. The variables are frequently renamed; the identity of the original puzzle beneath however, cannot be masked. Some might call it “Einstein’s Puzzle”, the “Zebra Puzzle” or with Creative Computing – the “People & Cabins Puzzle”. The first and perhaps only Web page besides my own (as far as I am aware), that discussed solving the puzzle with computer programming came from a 2004 page (since updated) by Lauri Karttunen. [2/10/2014 – this link to Lauri’s paper now appears to be dead]
The Einstein puzzle, weather originally his or falsely attributed to him is outwardly simple but deceivingly complex. Suggestions that 98% of the population would be unable to solve it may be conceited but it seems realistic that that amount could never be prevailed upon to try. The reader is encouraged to take a stab at solving this puzzle, in one of its various forms, without looking for answers or cheats. He or she might then gain an appreciation for the analysis required when contemplating such cognitive problem solving task.
So the following discussion explains how I approached the task; not how a similar task should be approached by more modern and more sophisticated techniques. It is an explanation of my image at the top of this page. This brief explanation is divided into three parts; analyzing the task, representing the information and identifying a framework of routines working within the algorithm.
Analyzing the task
Einstein’s riddle has thirty elements ((position, color, nationality, smokes, drinks and pets)x5). The statistical formula for Combinations of N objects taken K at a time is : C = N! / K! x ( N — K )! ……[ ” ! ” symbolizes factorial, 6! = 6x5x4x3x2x1 or 720 ]. The number of combinations (not permutations) for this puzzle should equal 30 elements taken 6 at a time [or] 30! / 6! X ( 30—6)! [or] 593,775 possible combinations ! Somebody please check my math.
Half a million combinations is a small number for a computer to chew when you consider numbers in the game of chess. “The number of possible chess positions, assuming that no pawn has yet been promoted, is roughly 10 to the 43rd. power”. “For Chess the number of games (games alone) lasting for 40 moves (assuming an average choice of 30 moves per position) is 10 to the 120th. power, which is far more than the number of atoms in the universe” ! { Chess and Computers by David Levy, p.39, 1976 } A slight exaggeration perhaps but an effectively infinite number nonetheless.
Representing the information
This was the hardest obstacle to overcome and once a decision was made on how to represent the data, then the rest sort of – fell into place. Back in 1979 -80 the available tools on my PC were integer and floating point BASICs (Beginner’s All Purpose Instruction Code), 6502 (Motorola) assembly language and the grandaddy of all spreadsheets – VisiCalc. (Pascal for the Apple II became available in 1979, also). My choice for representing data consisted of using BASIC’s multi-dimensional numeric arrays, coupled with logical AND, OR and NOT functions. Assembly language however, offered an elegant means of emulating arrays, simple logic functions and extremely swift speed. A spreadsheet application could have likewise been drafted to manipulate the puzzle data and perform logic functions.

 <click to enlarge>< or open/close and open a 2nd time to view full screen>
<click to enlarge>< or open/close and open a 2nd time to view full screen>
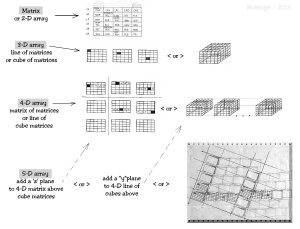
– A matrix will be defined as a 2—dimensional array. Probably the simplest way to describe the solution set for this puzzle is with a matrix.
– A 3-dimensional array can be described as a set of matrices in a row or as a stack of cells with depth.
– A 4 –dimensional array can be visualized as matrix containing smaller matrices as cells or as a row of 3-dimensional arrays.
– A 5-D array visualization of a numeric array is easily drawn by expanding models of the third or forth dimension. By now there are 5 polar coordinates within the array C%(v,w,z,y,x). In BASIC, C% would denote a numeric variable vs C$ that would denote an alphanumeric string variable.
– A 6-D visualization has already been presented – as the beginning image; the full sized image is thumbnailed just below. Interpretation for image below: {A fact is represented as a dark block in the solution set (frontal 2-dim. matrix), Succeeding test matrices carry over flagged values for row or column—shown in lighter shades. Additional facts add more flags further reducing the number of possible combinations. Eventually a routine to guess might be necessary—where results must match non-flagged cells.}
– One could carry this dimensional visualization process further. You could print duplicates of the 6-D image and place them in a row for the 7th.-dimension, a row and a column for the 8th., and then in a stack with depth for the 9th. Beyond that the visualization might become fuzzy, but the mathematical aspect is still easy to describe.
Framework of routines
Another programmer might have stopped at the 2-dimensional model where data continually shuffled in and out of one packed two dimensional solution matrix. A multi-dimensional array of the 6th.-dimension however is spacious enough to keep track of the numerous ’non possibilities’ in Einstein’s Riddle (remember there are 593,774 of those).
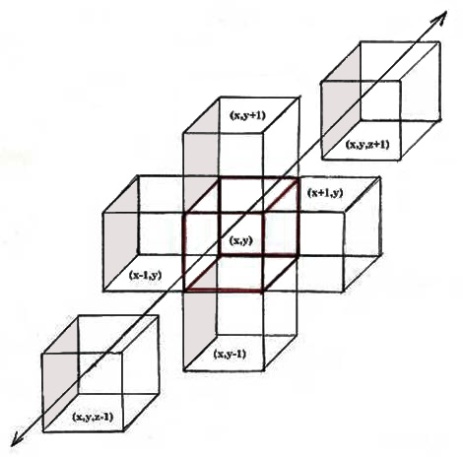
In my model C%(p,v,w,z,x,y) was used to describe any particular cell within the array where the “%” caricature denotes a numeric variable (either -1, 0, or +1). Logical comparisons of proximity were made at the simple and fundamental (z,x,y) polar coordinate level where only adjacent cells are evaluated. C%(p,v,w,z,x,y) = 1 is a positive correlation and C%(p,v,w,z,x,y) = -1 is a negative or non possibility. Variables for the Creative Computing puzzle were: p= position (left to right) / v=color / w=nationality / z=liquor / x=ammunition / y=duck.
With a model or framework to work with, what remained was to develop routines that sort of mimic the human thought process. Surprisingly this aspect was straight forward and fairly easy to do. Only about 7 or so subroutines were needed.
1. A routine to seed an array with the given clues that are accepted as facts.
2. A routine to evaluate proximity for the statement “this is next to that” or “this is to the left of that”.
3. A routine to establish non-relationships (ex: if not this, then not that).
4. A routine to seed the remainder of a row or column in an array with flags after a fact has been determined (flags mark non-possibilities).
5. A routine to increment elements, compare flagging, post any valid combinations.
6. A routine to check if solution is found, stop program and post success.
7. Finally a routine to make a guess and act accordingly if the above routines fail to complete the solution. A guess routine was actually unnecessary to solve this puzzle – but given one less clew it might have been.
So yes my BASIC program eventually solved the puzzle, printing out either 1’s or 0’s in 5 little (6 x 5) matrices on the screen. Execution of the program took over a minute in the interpreted BASIC through a processor running at less than 1MHz. Obviously I had to interpret the results. It was no great achievement in the annals of computing history, but a satisfying abet somewhat anticlimactic achievement for a self taught programmer.